128. — LETTRES À CONDORCET.
[Correspondance publiée par M. Henry, p. 80 et s.]
IX. (Divers objets. — Le commerce des grains.)
6 avril[1].
Il est vrai, M., que j’étais triste en quittant Paris, et je le suis encore. Je n’ai point à craindre les chagrins de l’ambition mais la sensibilité que j’aurais eue pour cet objet, s’est trouvée au profit de l’amitié, et lorsque je quitte mes amis, je suis aussi triste qu’un ministre exilé. Je verrai avec bien du plaisir ce que vous voudrez m’écrire sur la physique ou sur l’économie politique. Je vous parlerai la première fois des raisons que je crois avoir de préférer à tout la manière de juger par jurés[2]. Au reste, il est bien sûr que ce ne sera pour nous qu’un objet de spéculation. Nous aurons, ou nos tribunaux ordinaires, ou des tribunaux composés de juges amovibles et pensionnés.
Le pays où je me trouve à présent ne souffre point de la cherté des vivres comme celui que vous habitez ; le blé y est cher ; mais il y en a, et plus qu’il n’en faut pour le nourrir. L’édit de 1764 a fait défricher beaucoup de terres, et l’usage de cendres minérales qu’on a découvertes dans les environs de La Fère a mis à portée d’avoir des prairies artificielles ; mais on craint beaucoup la nouvelle année ici.
En 1764, l’agriculture languissait, beaucoup de fermiers étaient ruinés ; ils se sont relevés depuis. Peut-être, dans peu d’années, tout sera-t-il pis encore qu’en 1764. Je vais constater, pour un petit canton, la différence de l’état actuel à celui de 1764 ; il est bon qu’il reste des preuves du changement qu’a produit l’exportation.
Adieu, M., je voudrais bien vous voir à Paris à mon premier voyage ; il y a longtemps, mais bien longtemps, que je ne vous ai vu[3].
X. (Divers objets. — Utilité sociale de l’étude. — La Bible).
Ussel, 21 juin.
J’ai reçu, M., votre lettre du 14 timbrée de Chauny. Quoi que vous en disiez, je crois la satisfaction résultante de l’étude supérieure à celle de tout autre satisfaction[4]. Je suis très convaincu qu’on peut être, par elle, mille fois plus utile aux hommes que dans toutes nos places subalternes, où l’on se tourmente, et souvent sans réussir, pour faire quelques petits biens, tandis qu’on est l’instrument forcé de très grands maux. Tous ces petits biens sont passagers, et la lumière qu’un homme de lettres peut répandre, doit tôt ou tard détruire tous les maux artificiels de l’espèce humaine et la faire jouir de tous les biens que la nature lui offre. Je sais bien qu’avec cela il restera encore des maux physiques et des chagrins moraux qu’il faudra supporter en pliant la tête sous la nécessité. Mais le genre humain gagnerait beaucoup à s’abonner à ceux-là. Je vous avoue que la goutte ne m’a point empêché de continuer à croire aux causes finales. Je savais bien qu’aucun individu ni même aucune espèce n’était le centre du système des causes finales et que l’ensemble de ce système n’est, ni ne peut être, connu de nous. Cracher du sang, tousser, avoir la goutte, pleurer ses amis, tout cela n’est que l’exécution en détail de l’arrêt de mort prononcé contre tout ce qui naît ; et si nous ne mourons que pour renaître, il sera vrai encore que la somme des biens sera supérieure à celle des maux, toujours en mettant à part les maux que les hommes se font à eux-mêmes, maux passagers, à ce que je crois, pour l’espèce et qui le seraient aussi pour l’individu, si l’individu pensant et sentant avait plusieurs carrières successives à parcourir.
Je me flatte que ceux qui pourront un jour naître Limousins ne seront pas privés de la commodité des hottes, grâce au soin que vous voulez bien prendre de nous envoyer un vannier[5]. Je vous remercie du madrigal de l’abbé Arnauld, dont la pensée est agréable, mais les vers un peu duriuscules.
J’ai reçu de Genève un morceau sur les probabilités[6], qui est une espèce de plaidoyer pour M. de Morangiès. Cela vaut mieux que de faire des vers au vieil Alcibiade[7]. J’avoue que je ne pardonne pas non plus aux Académiciens d’avoir été dîner chez ce fat suranné, devenu délateur de ses confrères. Je persiste à croire que le choix de M. de Bréquigny[8], en pareille circonstance, est un acte de timidité qui ne fera qu’enhardir et fortifier le parti des faux-frères.
Adieu, M., conservez-moi votre amitié.
J’ai vu un Commentaire sur la Bible par Émilie[9], mais il n’avait que 2 volumes in-4°. Il a pu faire la pelote de neige entre les mains de son jeune amant[10] et du vieux de la Montagne[11]. Ce serait une chose intéressante qu’un pareil commentaire ; mais je le voudrais fait sans passion, et de façon à tirer aussi du texte tout ce qu’on en peut tirer d’utile comme monument historique précieux à beaucoup d’égards. L’envie d’y trouver des absurdités et des ridicules qui, quelquefois n’y sont pas, diminue l’effet des absurdités qui y sont réellement, et en assez grand nombre, pour qu’on n’en cherche pas plus qu’il y en a.
XI. (Détails divers. — La sparterie. — Aurore boréale. — L’abbé Raynal.)
Limoges, 14 juillet.
J’ai bien des reproches à me faire, M., car il y a bien longtemps que je ne vous ai écrit, et quoique, d’un côté, ce ne soit pas tout à fait ma faute et que, de l’autre, je vous connaisse indulgent, il est toujours fâcheux de ne pas répondre, comme on le voudrait, non pas à l’amitié, mais aux témoignages qu’on en reçoit.
J’attends votre vannier qui sans doute est parti, car je n’imagine pas que vous ayez suspendu son départ, et que vous ayez douté de l’acceptation de vos conditions. Je ferai mon possible pour qu’il soit content et pour tirer parti du talent de sa femme. S’il arrive pendant le petit séjour que je vais faire à Verteuil, il s’adressera à l’Ingénieur de la Province, M. Tresaguet. J’ai pris le parti, pour votre graine de raves, de l’envoyer sous une double enveloppe à M. Bertin, et j’ai prié Mlle de Lespinasse de lui demander la permission.
J’ai été fort content des Cabales et des Systèmes[12], à quelques bagatelles près. On a beau dire ; cet homme ne vieillit point, et donne le démenti à son extrait baptistaire pour mieux le donner à son baptême.
Avez-vous eu des orages comme nous et des grêles épouvantables ? Nous avons aussi eu des aurores boréales très fréquentes, mais je les ai peu observées, parce que pendant mes courses, je me couchais de très bonne heure. J’en ai pourtant remarqué une le 28 juin sur les dix heures du soir, à Limoges, d’autant plus remarquable qu’elle ressemblait très peu aux aurores boréales ordinaires. Ce n’était qu’une clarté blanchâtre qui tapissait le fond du ciel et qu’on apercevait à travers les nuages légers dont le ciel était parsemé, et qui rendaient, comme on dit, le temps pommelé. Mais les nuages semblaient être le fond, parce qu’ils étaient obscurs, et c’était le fond blanchâtre entrecoupé qui formait l’apparence d’un ciel pommelé. Une autre particularité de cette aurore boréale, c’est qu’elle était principalement répandue vers le Sud, quoiqu’il y eût dans la partie sereine du ciel quelques colonnes lumineuses qui rasaient la Grande Ourse.
J’ai souvent vu des nuages bordés de blanc, comme s’ils avaient été éclairés par la lune, quoiqu’elle ne fût pas sur l’horizon. J’ai vu aussi des nuages blanchâtres isolés dans des parties du ciel fort éloignées du Nord. Une fois, c’était, je crois, le 18 février 1764, j’ai vu une espèce de bande lumineuse qui s’étendait presque d’un bout à l’autre de l’horizon, et qui était d’une largeur à peu près égale partout. Elle suivait à peu près la direction du zodiaque, et n’était point la lumière zodiacale : 1° parce qu’elle était détachée de l’horizon ; 2° parce qu’elle était beaucoup plus étendue ; 3° parce que sa largeur était uniforme et qu’elle ne se terminait pas en pointe ; 4° parce qu’elle avait un mouvement parallèle à elle-même assez lent, mais très sensible. Je ne me souviens plus si c’était au Midi ou au Nord. Plus je vois ce phénomène et les différentes formes qu’il prend, plus je me convaincs que ce sont de véritables nuages qui n’appartiennent qu’aux parties les plus élevées de l’atmosphère, et que la matière qui les compose s’enflamme par une combustion réelle, tantôt lente et paisible comme celle du charbon, tantôt rapide et se communiquant au loin, comme dans la flamme et dans des traînées de matières combustibles. Je ne serais pas surpris que ces inflammations eussent quelques rapports avec le fluide électrique, fluide expansible qui doit s’étendre beaucoup plus haut que l’air, et qui, certainement, est chargé de beaucoup de phlogistique, qui, peut-être, est l’intermède par lequel le phlogistique que le soleil nous envoie se combine avec les corps solides et fluides où nous le trouvons. Peut-être est-il aussi l’intermède par lequel la chaleur écarte les parties mêmes de l’air et des autres corps devenus expansibles par la vaporisation. L’affectation des aurores boréales à occuper la partie septentrionale du ciel tiendrait à un mouvement que je soupçonne depuis longtemps dans la partie supérieure de l’atmosphère, de l’équateur au pôle, et qui me paraît une suite nécessaire de son expansibilité combinée avec la force centrifuge et la pesanteur. Il y a bien longtemps qu’il m’a passé par la tête d’expliquer par là le mouvement du fluide magnétique ; mais les faits relatifs à ce magnétisme sont encore trop peu connus et trop peu analysés. Pardon de vous faire part de mes rêveries ; j’oublie que les géomètres n’aiment pas les systèmes, et qu’il leur faut des calculs. Malheureusement, je n’en sais pas faire et mon imagination s’égare sans frein.
Mlle de Lespinasse m’apprend que vous travaillez sur quelque objet de littérature ; je ne crois pas qu’il y ait d’indiscrétion à vous demander sur quoi.
Je viens enfin d’achever l’Histoire des Deux-Indes. En admirant la facilité et la brillante énergie du style de l’auteur, je vous avoue que je suis un peu fatigué des excursions multipliées et des paradoxes incohérents qu’il rassemble de toutes les parties de l’horizon ; il entasse ceux de tous les auteurs les plus paradoxaux et les plus opposés, tous les systèmes moraux, immoraux, libertins, romanesques ; tout est également revêtu des couleurs de son éloquence et soutenu avec la même chaleur : aussi, ne résulte-t-il rien de son livre. Je voudrais aussi qu’il s’abstînt de déraisonner physique. Il aurait souvent besoin qu’on lui donnât le même avis que vous avez donné à La Harpe, lorsque celui-ci définissait l’octaèdre, une figure à huit angles.
Adieu, M., donnez-moi quelquefois de vos nouvelles et de celles des choses qui vous intéressent, sans user de représailles avec moi.
XII. (Détails divers. — La sparterie. — Mathématiques. — La cristallisation.)
Limoges, 27 octobre.
Je me reproche, M., un bien long silence avec vous. Mes courses en ont été en partie la cause : m’en voilà revenu depuis samedi et fixé ici pour quelque temps et, d’ici à mon retour à Paris, quelque impatience que j’aie d’y arriver, j’imagine que vous y y serez avant moi, ne fût-ce que pour terminer l’affaire du secrétariat[13] qui, ce me semble, devait l’être à la Saint-Martin. J’ai grand désir que ce soit une chose faite et non à faire.
J’ai traité hier à leur passage MM. du Régiment royal de Pologne, parmi lesquels était M. votre cousin orné d’une moustache qui le rend très vénérable et sur laquelle je lui ai promis de vous faire mon compliment.
Votre vannier commence à faire des hottes ; mais il ne sait point faire de vans. J’ai trouvé au reste ses demandes plus considérables que les conditions que vous m’aviez annoncées par votre lettre du 26 juin. Il demande un écu par jour au lieu de quarante sols et trois ou même quatre louis au lieu de deux pour son voyage. Sur ce que je lui ai fait observer cette différence, il m’a répondu que ce n’était pas avec lui que vous aviez traité, mais avec son jeune frère, lequel avait craint de s’éloigner si fort de sa patrie et d’aller vivre parmi des barbares, que lui, plus aguerri aux dangers des voyages, avait pris sur lui de faire honneur aux engagements de son frère, mais qu’il n’avait rien fixé sur le prix. Je suis convenu avec lui que je vous en écrirais et que je m’en rapporterais entièrement à ce que vous décideriez. Dans le vrai, les meilleurs ouvriers de ce pays-ci, ne gagnent pas quarante sols et le sieur Fondemant est très bien nourri pour vingt sols et d’ailleurs logé.
Je vous remercie bien de votre formule[14], quoiqu’elle soit arrivée lorsque je n’en avais plus besoin, m’étant procuré un moyen équivalent pour arriver au même but, par une règle arithmétique fondée sur les mêmes principes. De plus, je m’étais aperçu que je ne pouvais en tirer aucune utilité pour l’objet que je me proposais. Je supposais que l’on pouvait, par une division toujours poussée plus loin, augmenter indéfiniment l’espace occupé par une quantité de matière quelconque et je voulais rechercher suivant quelle loi et pour cela je supposais une boule inscrite dans un tétraèdre et occupant l’espace qu’il renferme.
Je la supposais divisée successivement en quatre, dix, vingt et autres nombres pyramidaux, mais je n’ai pas tardé à m’apercevoir de ce que j’aurais dû prévoir dès le premier moment, c’est que le tétraèdre renfermant les quatre boules était plus petit que celui qui n’avait qu’une seule sphère, et qu’ainsi, au lieu de gagner du terrain, j’en perdais. Je me souviens pourtant d’avoir lu autrefois dans Keill[15] ou Gravesande[16] un beau théorème de Newton, d’où il résulte qu’avec un pouce cube de matière, on peut remplir toute la sphère qui a pour rayon celui de l’orbite de Saturne. S’il y a des vides tels que les corps ne se touchent pas les uns les autres, ou si l’on dispose la matière en figures creuses, il n’y a rien de bien merveilleux. M. de Morveau rappelle l’énoncé de ce théorème, mais il n’en donne d’ailleurs aucune idée, et je ne me souviens plus du tout de la manière dont Newton dispose la matière pour obtenir son résultat.
J’ai, à propos de boules, un beau problème à vous proposer ; mais cela demande quelque explication et je n’aurai pas le temps ce soir.
Je ne suis pas plus en droit que M. de Romé de faire les honneurs de la géométrie, mais j’ai bien peur qu’il n’ait trop raison quand il dit que la géométrie ne pourra jamais expliquer ce phénomène[17]. Ce n’est pas qu’il ne gise, comme toute la physique, in pondère et mensura ; mais les mouvements se passent trop hors de notre portée et nous n’en voyons que des résultats trop éloignés et trop compliqués pour que nous puissions remonter aux causes. La seule tendance des parties de l’eau qui se gèle à s’assembler sous des angles de 60°, qui peut-être est, de tous les phénomènes relatifs à la cristallisation, le plus simple, n’a-t-elle pas de quoi confondre toutes les recherches ? Quelle figure faudra-t-il supposer aux unités du fluide aqueux ? Il n’en existe aucune possible qui ait tous ses angles de 60° ; le tétraèdre, l’octaèdre, formés par des triangles équilatéraux n’ont aucune de leurs faces qui se joignent sous cet angle. Supposera-t-on de petits parallélépipèdes d’une hauteur presque nulle et ayant pour base un losange composé de deux triangles équilatéraux ? Comment concilier cette figure avec l’idée d’un fluide, avec le mouvement de fluidité, avec tous les phénomènes que présente l’eau. D’ailleurs, comment expliquer l’inclinaison dans tous les sens des lames qui s’enfoncent dans le fluide et de celles qui s’élèvent en s’inclinant sur la surface de l’eau. La figure supposée n’expliquerait que la formation des filets sur la surface même de l’eau ; et les lames inclinées les unes aux autres, et aux parois du vase, sous l’angle de 60°, devraient d’ailleurs nager à plat sur la surface de l’eau. C’est ce qui n’arrive pas. Autre mystère : Supposerez-vous l’élément ou l’unité insensible semblable au cristal sensible ? Dans le fait, le plus petit cristal ressemble au plus grand. Mais comment l’assemblage de ces petits cristaux en formera-t-il un grand sensible à ses éléments ? Il y en a dont la figure est un tétraèdre ; d’autres, dont la figure est octaèdre ; d’autres, en très grand nombre, composés de prismes hexagonaux terminés par une pyramide hexagonale. Aucune de ces figures ne peut, en s’assemblant, remplir un espace, ni former une figure semblable à la première. Il faudrait pour cela des cubes ou des prismes hexagonaux terminés par trois rhomboïdes comme les cellules des abeilles. Mais, même avec le cube, comment expliquer la formation du cristal de sel marin ? Comment, lorsque dans l’évaporation insensible, lorsque le petit cube élémentaire de Rouelle est devenu la pointe d’une pyramide renversée, cette pyramide retombée enfin dans la liqueur s’y reforme-t-elle en cube ? Comment tous les vides se remplissent-ils et pourquoi tous les cubes qui se déposent à la surface de la pyramide ne s’arrangent-ils pas en la couvrant couche par couche et en lui conservant sa figure primitive ? Comment la figure cubique se rétablit-elle après avoir été dérangée et même en laissant des vides qui ne sont point remplis ? Ces fluides et, bien plus encore, des interruptions des corps étrangers qui sont au milieu d’un cristal doivent déranger l’effet de l’attraction. Cependant la forme du cristal se retrouve. Les cristaux de nitre ont toujours six pans ; mais quelquefois, ces cristaux sont aplatis de façon à former une espèce de table de deux faces opposées, tandis que les quatre autres ne forment qu’une espèce de double biseau. Dans les cristaux de roche, on trouve souvent des quilles qui traversent d’autres quilles en se pénétrant et se confondant en partie et qui, cependant, sont toutes deux régulières. Tout cela confond le chimiste et le géomètre ; mais le chimiste se borne à observer. Le géomètre qui parviendrait à expliquer, serait, je crois, le véritable sorcier.
Adieu, M., j’aurais encore bien des choses à vous dire, mais ma lettre ne partirait pas. Vous savez combien vous devez compter sur mon amitié.
Mlle de Lespinasse m’a mandé l’extrémité de M. D’Ussé et je crains bien que vous ne l’ayez déjà perdu. Vous ne doutez pas de la part que je prends à ce que cet événement a de douloureux pour vous.
XIII. (La cristallisation.)
Limoges, 6 novembre.
Voici, M., le problème dont je vous ai parlé dans ma dernière lettre.
Si l’on suppose un nombre indéfini de sphères d’un diamètre égal, parfaitement dures, parfaitement lisses, d’une densité égale, on convient, ce me semble, que leur assemblage a toutes les propriétés des fluides. Si l’on n’en convient pas, il est bon de rechercher avant tout si la chose est vraie et démontrable et si l’on pourrait dans ce cas démontrer à priori le principe de l’égalité de pression. Quoi qu’il en soit, si, en effet, il est démontré qu’un assemblage de sphères ainsi constitué formerait un fluide, bien entendu que cet assemblage soit assez vaste pour que ses dimensions n’aient qu’un rapport inassignable avec le diamètre des sphères, car sans cela, on conçoit aisément que leur jeu ne serait plus libre. Tout cela supposé, je dis que si, dans cet assemblage de sphères, on interpose d’autres sphères aussi en nombre indéfini dont le diamètre soit différent, le fluide cessera d’être aussi fluide que si l’on ne mêle deux, trois, quatre ordres de boules ; l’assemblage prendra une solidité toujours plus grande et qu’il y a tel assemblage de tel nombre d’ordres différents de boules, avec un tel rapport de nombre entre leurs différents diamètres, qui rendent l’assemblage capable de résister à une force donnée. C’est l’expérience de ce qui se passe dans la confection des routes qui m’a conduit à cette théorie. Il est certain que des cailloux ronds d’un ou deux pouces de diamètre répandus sur un chemin roulent les uns sur les autres et que le chemin n’a aucune solidité jusqu’à ce qu’une partie ait été broyée par le passage des voitures. Un chemin de sable pur n’est pas plus solide et les roues y font des ornières profondes. Mais si ce même sable et ces mêmes cailloux sont mêlés ensemble dans une certaine proportion que l’expérience fait connaître et qui varie suivant la finesse du sable et les dimensions des cailloux, il en résulte de toutes les espèces de chemins le plus solide et le plus inaltérable. Il me paraît que cet effet vient de ce que le caillou qui est immédiatement pressé par la roue d’une voiture a, par le moyen de l’interposition du sable, une plus grande masse de cailloux et de sable à déplacer que s’il était seulement environné de cailloux égaux et du même diamètre que lui. Il me semble que le sable, par sa plus grande division et par l’espèce de fluidité qui en résulte, distribue au loin l’action du fardeau et le partage entre un plus grand nombre de boules. Mais ce n’est là qu’une vue infiniment vague. Je doute fort que la solution du problème soit possible, surtout si on l’envisage dans sa généralité ; le nombre des ordres, les diamètres des boules, leur pesanteur spécifique sont trois éléments susceptibles chacun de varier à l’infini et de compliquer peut-être le problème au point de le rendre insoluble. Mais peut-être pourrait-on en examiner quelque cas particulier et en tirer des considérations utiles et applicables à quelques points de physique. Au pis aller, vous excuserez mon ignorance qui ne me permet pas de distinguer nettement les limites du possible et de l’impossible.
Adieu, M., vous connaissez toute mon amitié. Je vous adresse ma lettre à Paris, vous croyant bien près de votre retour. Je crois vous avoir fait mon compliment sur la perte de M. d’Ussé sur laquelle je partage vos regrets et ceux de Mlle de Lespinasse. Vous n’avez pas eu, comme elle, la douleur de le voir souffrir.
XIV. (La cristallisation.)
Limoges, 13 novembre.
Je suis fort aise, M., que vous me donniez des armes contre les prétentions exorbitantes de votre vannier ; je ne veux pas lui tenir rigueur, mais ce qu’il aura de plus que vos premières conventions sera une grâce.
J’ai oublié dans la grande lettre que je vous ai écrite dernièrement la chose la plus essentielle et pour laquelle précisément je vous écrivais, c’est-à-dire l’énoncé de mon problème. Vous y aurez facilement suppléé. Quoi qu’il en soit, on peut l’envisager de deux manières ; l’une particulière et l’autre plus générale. On peut, étant donnés, un, deux ou trois ordres de boule, de différents diamètres et pesanteurs spécifiques donnés et mélangés dans une proportion donnée, examiner le rapport de la résistance de l’agrégat qui en résulterait avec celle de l’agrégat formé par un seul ordre de boules, ou bien l’on peut demander quel est le nombre d’ordres de boules, la proportion des diamètres et des mélanges qui donnera le maximum de résistance. Je crains fort que ces problèmes ne soient trop compliqués.
Ils le sont pourtant bien moins que ceux qu’il faudrait résoudre pour expliquer le phénomène de la cristallisation. Je ne suis pas du tout battu par votre comparaison de Thalès et de Pythagore auxquels on aurait proposé le problème de la précession des équinoxes à résoudre et qui auraient eu tort de conclure de leur impuissance à l’impossibilité de la chose. L’astronomie physique s’est prêtée au calcul parce qu’on y voit ce qu’il y a à calculer ; tous les mouvements et les distances des corps célestes, leurs figures mêmes, sont données par l’observation. Dans les phénomènes de la chimie, au contraire, tout se passe hors de la portée de nos sens et nous n’avons point de prise pour connaître ni les figures, ni les mouvements ; nous ne voyons que des résultats infiniment compliqués dont les causes sont non seulement trop éloignées de l’effet, non seulement en nombre presque infini, mais, ce qu’il y a de pis, en nombre inconnu, puisqu’il est démontré qu’il y a plusieurs fluides plus subtils que l’air qui sont absolument incoercibles et qui peuvent entrer comme principes dans les combinaisons des mixtes. Je n’ai pas assurément prétendu épuiser les hypothèses, même pour le cas de l’eau glacée, mais elle indique cependant la forme de triangle équilatéral, et comment arranger cette forme avec les propriétés d’un fluide. Je vous ai fait grâce de la manière dont les grands cristaux se forment par lames parallèles et cependant conservent la forme hexagone. Vous me dites que les corps qui se cristallisent sont composés ; oui, les unités du mixte. Mais c’est l’agrégat composé d’un nombre immense d’unités dont nous voyons la cristallisation, et la difficulté consiste à expliquer comment la même figure se retrouve dans l’agrégat, quel que soit le nombre d’unités dont il est composé. Adieu, M., le papier me manque. Recevez les assurances de mon amitié. Je suis charmé de vous savoir à Paris.
XV. (Détails divers. — Le phlogistique ; l’éther. — L’air fixe.)
Limoges, 27 novembre.
L’Histoire de l’Académie ou des Académiciens morts avant 1699 me paraît devoir être un morceau intéressant quoiqu’à quelques égards ce soit étaler notre pauvreté, car il faut avouer qu’à cette époque nous étions prodigieusement inférieurs dans les sciences aux Anglais, dont c’était le bon temps, et même aux Allemands. Il y avait pourtant quelques gens de mérite. Je ne me souviens plus si Fontenelle a fait l’éloge d’Huyghens ; il me semble que non. En ce cas, ce sera un éloge principal à traiter. Ce qui me fâche de cet ouvrage, c’est qu’il ne laisse pas de demander des recherches et des lectures de livres qu’on ne lit plus guère, qu’il exige, par conséquent, du temps pour être bien fait. Or, je voudrais que votre affaire fût décidée promptement.
Vous aurez à discuter s’il est vrai que Roberval et Frenicle aient eu, avant Newton, l’idée d’expliquer toute l’astronomie physique par la gravitation universelle. Quand cela serait vrai, cela n’ôterait guère à la gloire de Newton, car de cette première idée à l’exécution, il y a une bien prodigieuse distance ; il y a toute celle de Frenicle à Newton.
À propos de Newton, je viens de lire dans un journal anglais, un moyen fort ingénieux pour expliquer comment il a pu ne pas s’apercevoir de l’inégale dispersion des rayons dans la réfraction de l’eau et du flintglass, quoiqu’il ait fait l’expérience d’où on l’a conclue. C’est un moyen de sauver son infaillibilité, dont l’idée est due à un M. Mitchell. La voici : elle consiste à supposer, ce qui, je crois, est fondé sur quelques textes de l’optique, que pour augmenter la force réfractive de l’eau, Newton y mêlait des sels et en particulier du sel de Saturne. Or, a dit M. Mitchell, il est très probable que le plomb dissous dans l’eau sous la forme de sel aura le même effet d’augmenter la propriété dispersive des rayons qu’il a lorsqu’il est combiné avec le sable dans le flintglass. M. Mitchell a répété l’expérience de Newton avec de l’eau imprégnée de sel de Saturne et il a vu qu’effectivement la dispersion des rayons se compensait à peu près, en sorte que l’image, qui avait traversé les deux prismes disposés en sens contraire n’était pas sensiblement troublée, ainsi que Newton l’avait remarqué. Dollond[18], ayant fait l’expérience avec de l’eau simple et du flintglass a dû voir l’effet tout différemment. Cette explication m’a fait plaisir, car j’aime et vénère la mémoire de Newton.
Quand votre expérience ne réussirait pas, je n’en croirais pas davantage à la prétendue légèreté spécifique du phlogistique dans l’air. Encore, si M. de Morveau au lieu de parler de l’air, eût parlé de l’éther, de ce fluide ou de ces fluides plus subtils que l’air, qui passent à travers les pores des corps, comme le fluide électrique, le fluide magnétique, le fluide qu’il faut supposer pour expliquer comment la chaleur produit entre les éléments de l’air, de l’eau en vapeur, du mercure, du cuivre en vapeur — cette répulsion en raison inverse des distances, d’où résulte l’état de vaporisation ou de fluide expansible — on pourrait l’écouter, car il pourrait supposer que le volume du tissu spongieux que formeraient également dans un pareil fluide la litharge et le plomb revivifié, serait augmenté plus que sa pesanteur par l’introduction du phlogistique, à peu près comme si l’on empâtait avec de la cire fondue une masse de limaille de fer d’un pied cube ou, si vous voulez, une masse de plomb en grains, le volume total apparent serait le même, mais le volume réel, celui qui correspondrait à l’eau déplacée, serait augmenté, et, comme la cire nage sur l’eau, la pesanteur relative du tout serait diminuée. Mais si l’on veut recourir à ces fluides, je dirai encore qu’il est très possible que ces différents fluides ou leurs éléments soient susceptibles d’entrer, ainsi que l’air, dans la combinaison des mixtes, d’en devenir principes ou d’être principiés, comme nos chimistes le disaient quelquefois de l’air, avant que nous eussions adopté des Écossais cette fausse et impropre dénomination d’air fixe qui donnerait à entendre que l’on a découvert une espèce d’air différente de l’air commun, comme l’ont, à ce que je crois, imaginé quelques-uns des Écossais qui ont travaillé sur cette matière. Il paraît qu’ils ont ignoré les travaux de nos chimistes et la doctrine de l’air combiné dans les mixtes, tantôt au point de saturation, tantôt avec surabondance, comme dans les eaux de Selters, dans le vin mousseux, etc., telle que l’a développée Venel et que Macquer l’a expliquée aussi dans son Dictionnaire de chimie. Ces messieurs avaient rappelé à une meilleure théorie et ils avaient étendu les conséquences des premières expériences de Stahl, lequel est vraiment le premier qui ait aperçu le rôle que l’air joue dans la nature comme principe des mixtes ; mais toutes les idées spéculatives de Stahl, toutes les conséquences qu’il tire des faits qu’il a vus, sont infiniment embrouillées et manquent de cette dialectique, de cette précision d’idées et de langage dont jusqu’ici les physiciens se sont occupés beaucoup trop peu et dont le défaut remplit leurs écrits de paralogismes, de paradoxes, de suppositions tacites d’où naissent des conséquences absurdes, etc., etc. Ce sont nos chimistes qui ont fait disparaître les paradoxes de cette doctrine, qui ont montré que l’air dans les corps solides n’était pas comprimé, mais combiné, que ce n’était ni à l’air, ni à l’eau que les corps solides devaient leur solidité, mais à l’union de leurs différents principes, à l’équilibre des tendances en vertu desquelles ces principes, en telle ou telle proposition, s’unissent pour former tel ou tel mixte et à la force des tendances qui sont, les unes vers les autres, les unités de ces mixtes ainsi formés. Ils ont remarqué que la fluidité liquide dans l’eau, la fluidité expansible dans l’air et dans l’eau en vapeur, étaient des propriétés appartenantes à l’agrégat et non aux unités des mixtes plus ou moins composés, plus ou moins simples, ou de leurs éléments, que ces propriétés avaient pour cause l’application de la chaleur et la force par laquelle elle tend à écarter les molécules des corps qu’elle pénètre, d’où il suit que cet effet est nul lorsque la tendance des molécules de l’agrégat les unes vers les autres ou la tendance des principes vers les autres principes du mixte surpasse la force d’écartement de la chaleur actuelle. Voyez l’article Chimie, dans l’Encyclopédie, l’article Effervescence des Mémoires de Venel sur les eaux de Selters et l’article Expansibilité (avec l’errata qui est au VIIe volume, sans lequel vous ne l’entendriez pas)[19]. Dans cette doctrine, l’air, combiné avec les corps, y est fixé par la combinaison ; il en est dégagé lorsque le mixte se décompose et qu’il s’en forme de nouveaux ; souvent, il se recombine sur-le-champ comme dans la fermentation du vin. Mais la dénomination de fixe ne lui convient point. Cette fixité n’est qu’un état accidentel et passager et non une propriété constitutive d’une substance particulière de l’air, distinguée de l’air commun.
Mais les Écossais sont venus ; ils ont cru découvrir ce que nous savions il y a plus de vingt ans, ce qui n’a pas peu contribué à l’enthousiasme avec lequel ils ont annoncé leurs découvertes. Ils y ont ajouté beaucoup d’expériences ingénieuses et intéressantes sur les effets de cet air récemment dégagé des mixtes auxquels il était uni ; ils ont observé que cet air, ainsi récemment dégagé, se recombinait plus aisément et qu’il avait différents effets qu’on ne pouvait point obtenir de l’air qui était depuis longtemps dans l’état d’agrégation expansible. Cette partie de leur doctrine est ce qui leur appartient ; elle est nouvelle, intéressante, féconde en belles expériences chimiques et peut-être médicales. Mais, s’ils en ont conclu que cet air était une autre substance que l’air commun, leur conclusion est plus étendue que les prémisses. L’air sur lequel ils opèrent n’est point de l’air fixe, mais bien de l’air qui a été fixé pendant quelque temps et qui ne l’est plus. C’est de l’air dégagé de la combinaison dans laquelle il avait été fixé. La dénomination d’air fixe est donc impropre et il faut la bannir. Au reste, les Anglais n’ont pas tant de torts que leurs traducteurs, car leur mot est : fixe d’air, ce qui peut se traduire par air fixé, aussi bien que par air fixe, mais encore ce mot d’air fixé ne donne-t-il pas une idée nette de la chose : cette chose est de l’air élémentaire considéré comme élément ou comme principe et non comme agrégat, lequel est tantôt fixé, tantôt dégagé, par la combinaison ou la décomposition des mixtes.
Pardon de cette digression occasionnée par l’humeur que m’a donnée : 1° l’introduction d’un langage impropre dans la physique déjà trop infectée de ce vice ; 2° l’emphase avec laquelle au moyen de cette dénomination impropre on a voulu nous persuader que quelques médecins d’Édimbourg avaient changé la face de la physique, lorsqu’ils n’ont fait qu’étendre des découvertes très connues, beaucoup plus intéressantes en elles-mêmes que la nouvelle extension qu’on leur a donnée et qui n’ont pas fait autant de bruit lorsqu’elles ont paru sous leur véritable nom, qu’elles en font aujourd’hui sous leur mauvais surnom.
Je reviens à votre projet d’expérience[20]. Elle me paraît très bien imaginée et devoir être concluante si, en effet, l’introduction dans l’eau de chaux d’un air qui se dégage d’autres substances fait précipiter par l’union de cet air avec l’eau la matière calcaire qu’elle tenait en dissolution.
Je ne connais ce fait que par le récit que vous m’en avez fait un jour et j’ai compris alors tout le contraire ; c’est-à-dire que l’eau ne pouvait dissoudre la chaux qu’autant que l’on rendait à cette chaux l’air qu’elle avait perdu avec son eau de cristallisation par l’opération de la calcination. Cela me paraissait se lier fort bien avec les expériences de Stahl qui, en calcinant la pierre sous son appareil, en a tiré beaucoup d’eau et beaucoup d’air ; c’était d’ailleurs une clef fort heureuse pour expliquer comment la dureté du mortier, n’étant due qu’à la régénération du spath calcaire qui, en se cristallisant, adhère aux parois que lui présentent les grains de sable ou de ciment avec lesquels la chaux est brassée ; comment ce spath calcaire régénéré, formant sous les voûtes en s’infiltrant à travers les joint des pierres, de véritables stalactites calcaires qu’on peut de nouveau réduire en chaux par le moyen du feu ; comment la chaux reprenant, lorsqu’on l’éteint, l’eau que le feu lui avait enlevée, il arrive cependant que la chaux qui se précipite conserve une onctuosité qui l’empêche de se sécher et de se mettre en une poudre friable, comme fait tout sel régénéré qui se cristallise au fond de l’eau ; comment cette onctuosité se conserve plusieurs années si la chaux est dans une fosse couverte, en sorte qu’elle n’en est que meilleure pour faire du mortier, tandis qu’on tenterait vainement d’en faire avec de la pierre calcaire réduite en poudre impalpable. Il faut donc qu’il y ait une grande différence entre la chaux éteinte et la pierre calcaire ou le spath calcaire recristallisé et servant de lien aux grains de sable dans le mortier. L’expérience que vous m’annonciez de la manière dont je la comprenais m’expliquait cette différence. Sans doute, disais-je, l’air n’est pas moins essentiel à la cristallisation du spath calcaire que l’eau. Il a perdu l’un et l’autre dans la calcination. L’extinction de la chaux n’a rendu à la terre calcaire que l’eau et peut-être seulement une partie de l’eau qu’elle avait perdue ; elle ne lui a point rendu cet air nécessaire à la constitution du spath calcaire et sans lequel il ne peut être ni dissous dans l’eau, ni cristallisé. Cet air ne peut lui être rendu que peu à peu, par le laps de temps, par la multiplication des surfaces exposées à l’air, par l’infiltration même successive des eaux qui contiennent toujours de l’air dans une certaine proportion et souvent avec surabondance. J’étais fort satisfait de cette théorie et vous venez la renverser par votre manière d’exposer l’effet de l’air dégagé appliqué à l’eau de chaux. Il me reste pourtant une ressource : c’est de supposer que l’eau chargée d’une surabondance d’air est moins propre à tenir le spath calcaire en dissolution, que par conséquent, celle à qui l’on fournit de nouvel air laisse précipiter une partie du spath qu’elle tenait dissous. Cette explication n’empêcherait pas que le défaut de solidité de la chaux récemment éteinte et son état d’onctuosité ne fussent dus au défaut de l’air qu’elle n’a point encore pu reprendre.
Il sera aisé de vérifier si c’est du spath calcaire régénéré ou simplement de la chaux, en état de chaux éteinte, que précipite l’air introduit surabondamment dans l’eau de chaux. Il n’y a qu’à examiner le précipité ; s’il est onctueux comme la chaux, s’il est propre à faire le bon mortier en le mêlant avec du sable ou de la terre cuite pilée, ma théorie ne vaut rien ; mais s’il se sèche, s’il est friable sous les doigts, s’il ne fait pas plus corps avec le sable que ne le ferait de la pierre calcaire réduite en poudre fine, ma théorie n’aura reçu aucune atteinte. Vous pourrez aisément faire cette expérience en même temps que la vôtre. Je serai charmé d’apprendre le résultat de toutes deux.
Je n’entends pas trop bien ce que vous me dites sur ces assemblages de sphères dont vous dites qu’il serait possible qu’aucun ne jouit de la propriété de l’égale résistance. Y comprenez-vous l’assemblage de sphères toutes égales ? J’en serais surpris, car il me semble que les physiciens conviennent assez, sans pourtant l’avoir rigoureusement démontré, qu’un pareil assemblage aurait toutes les propriétés d’un fluide. Il serait, ce me semble, également intéressant de démontrer que la chose est, ou de démontrer qu’elle n’est pas. Je vous dirai à ce sujet que les six hypothèses possibles à imaginer sur la composition des fluides sont en si petit nombre et si simples que j’ai toujours cru qu’on pourrait, si les difficultés analytiques ne s’y opposent pas, les examiner toutes et voir si l’on peut en déduire la propriété de l’égalité de pression. Si les six hypothèses donnent ce résultat, on aura démontré a priori le principe de l’égalité de pression et, par conséquent, toute la science du mouvement des fluides. Si quelques hypothèses s’y refusent et que les autres s’y prêtent, on aura restreint et fixé, par voie d’exclusion, le nombre des hypothèses qui peuvent avoir lieu dans la réalité.
Voilà tant de bavardage physique qu’il ne me reste guère de temps pour vous parler d’autre chose. Vous me donnez fort bonne idée de la Réponse d’Horace[21] ; il est mieux en secrétaire que Boileau, pas aussi bien cependant que Mlle de Lespinasse. Ce que tout le monde me mande de l’état où elle est m’inquiète véritablement. Je crains pour sa poitrine. J’espère être bientôt à portée de juger par moi-même de son état ; cependant, je ne puis encore fixer le temps de mon départ.
Adieu, M., chargez-vous, je vous prie, de tous mes compliments pour tous nos amis.
Cela ne vaut plus la peine de me rien envoyer que ce qui peut aller par la poste.
Je reçois votre lettre de mardi. M. Montagne[22] ajoutera toutes les démonstrations. Ce que vous me mandez de l’état de Mlle Lespinasse me désole.
XVI. (Détails divers.)
Limoges, 4 décembre.
J’attends l’Épître d’Horace avec impatience, M. ; j’imagine qu’elle arrivera ce soir. Pour les livres, cela ne vaut plus la peine de m’en envoyer ; je vous prierai seulement de me faire souscrire pour Montagne. Je préfère l’in-quarto.
Je n’ai point reçu les hardes du vannier, mais je les lui ferai remettre quand elles arriveront.
La toux de Mlle de Lespinasse m’inquiète beaucoup. Je voudrais qu’elle prît du lait, soit que sa toux soit de poitrine, soit qu’elle appartienne aux nerfs ; cela lui vaudrait mieux que de se bourrer de drogues.
Si les Lois de Minos[23] sont bien écrites, et la pièce intéressante, je leur pardonnerai le reste, attendu que, si la pièce est intéressante, les portraits seront d’imagination.
Adieu, M., j’ai encore plus d’impatience de savoir le résultat de votre expérience que d’avoir l’Épître d’Horace.
Recevez les assurances de ma bien sincère amitié.
XVII. (Les logarithmes. — Détails divers.)
Limoges, 13 décembre.
Je ne vous laisse pas tranquille, M., voici encore un nouveau problème qui serait utile pour un homme qui voudrait pousser les tables de logarithmes plus loin qu’elles ne le sont. Un homme qui habite Limoges y a pensé et a resserré l’espace en se bornant aux nombres premiers qui, comme on sait, sont les seuls nécessaires, les autres étant très faciles à suppléer. Il voudrait se servir de quelques calculateurs que j’ai dans mes bureaux qui calculent avec une facilité prodigieuse et dont il dirigerait et surveillerait les opérations.
Le travail qu’il faut faire, pour trouver le logarithme d’un seul nombre, rend cette entreprise épouvantable pour l’homme le plus patient et le plus intrépide et je ne conçois pas comment on en est venu à bout. Je me suis demandé s’il n’y aurait pas moyen d’abréger cet immense travail en le réduisant aux seuls calculs nécessaires pour trouver les moyens arithmétiques sans être obligé de faire les multiplications et les extractions de racines qui donnent les moyens géométriques correspondants.
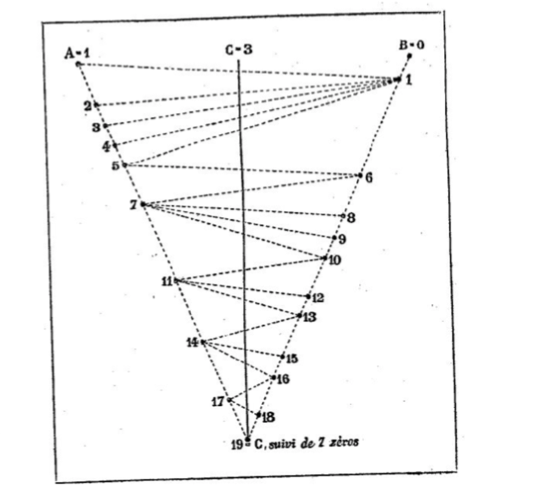
Voici mon idée : il n’est pas nécessaire de trouver ces moyens géométriques pour connaître l’ordre dans lequel on doit procéder pour chercher les moyens arithmétiques. Si l’on pouvait, par une formule, un nombre E étant donné, entre les deux extrêmes A et B, et la distance de ce nombre à ces deux extrêmes étant connue et exprimée en unités, trouver combien il faut chercher de moyens proportionnels géométriques pour arriver à un moyen qui soit le nombre E lui-même, suivi d’autant de zéros qu’on veut mettre de décimales au logarithme et trouver en même temps dans quel ordre ces moyens, successivement cherchés, passeraient alternativement au-dessus ou au-dessous du nombre E, on aurait tout ce qu’il faut pour chercher tous les moyens arithmétiques disposés dans le même ordre et dont le dernier serait le logarithme du nombre E. J’ai marqué dans la figure ci-après l’ordre que suivent les moyens géométriques qu’il faut trouver pour arriver au logarithme de 3 dans les tables ordinaires. Cette figure suffirait pour trouver ce logarithme en cherchant les moyens arithmétiques dans le même ordre, sans savoir quels sont ces moyens géométriques. Mais il faut former cette figure, et je crois qu’il doit être possible de donner pour cela une formule ; mais ce que je crains fort, c’est que le calcul et l’application n’en soient plus compliqués encore que l’opération même de la recherche des moyens géométriques ; c’est ce que je vous propose de chercher, si vous croyez que la chose en vaille la peine.
À propos de logarithmes, si vous êtes à la portée de voir les grandes tables de Wlac, je vous prie de m’envoyer : 1° le logarithme de 240 ; 2° le logarithme de 241 ; 3° les nombres qui répondent aux logarithmes de ces deux nombres multipliés par 84 ; bien entendu que la caractéristique sera réduite pour trouver les nombres dans les tables ; 4° les logarithmes des tables pour ces deux derniers nombres, avec les logarithmes des deux nombres suivants étant en tout six logarithmes et deux nombres, le tout écrit lisiblement. Je demande les logarithmes des tables de Wlac. J’ai celles de Rivard, mais je voudrais plus de chiffres pour plus d’exactitude.
Si à tout cela vous pouvez joindre l’Éloge de Racine, je vous en serai encore plus obligé. Vous me demandez quand donc je reviens ; je vous réponds que ce ne sera que les premiers jours de janvier, ce dont je suis bien fâché. Je viens d’avoir un petit ressentiment de goutte, mais c’est si peu de chose que je n’en serai point retardé.
Adieu, M., recevez les assurances de mon amitié. Mille respects à Mlle de Lespinasse et donnez-m’en des nouvelles.
XVIII. (Détails divers. — La calcination des métaux.)
Limoges, 21 décembre.
J’ai reçu, M., l’Épitre d’Horace, et je vous en fais d’autant plus de remerciements qu’elle m’a fait grand plaisir. Il y a une foule de vers très heureux, de la facilité, un ton fort et bon ; l’ouvrage marche bien. Je suis pourtant fâché que l’auteur ait justifié Horace de ses flatteries.
Je ne savais pas que les travaux du chimiste Duclos[24] vous donnassent l’occasion de parler de l’augmentation du poids des métaux calcinés. Je ne crois pas que cela vaille beaucoup la peine de parler de mes conjectures : 1° parce que, quoique Stahl et Lewis n’aient sur cela que des idées assez vagues, je vois cependant, par l’ouvrage de M. de Morveau, qu’ils ont l’un et l’autre eu l’idée d’attribuer cette augmentation à l’absorption de l’air ; 2° parce qu’une des inductions dont je me servais pour appuyer ma conjecture se trouve détruite par des expériences de M. de Morveau qui sont dans les Mémoires de l’Académie de Dijon. Je parle de celles que je fondais sur la nécessité du contact de l’air pour la combustion. M. de Morveau a fort bien prouvé que ce n’était pas l’air comme agent chimique qui était nécessaire à la combustion, mais l’air comme agent mécanique et doué d’une élasticité dont les vibrations alternatives, en comprimant plus ou moins le fluide igné entretient le mouvement de l’ignition. Cela ne me fait pas renoncer à mes idées, mais me fait désirer de les confirmer par des expériences. J’ai imaginé un appareil pour calciner les métaux dans les vaisseaux fermés et pour mesurer l’absorption de l’air. Nous en causerons à Paris. Il faudrait malheureusement du loisir et un local commode pour exécuter ces expériences, dont l’appareil serait d’ailleurs un peu coûteux.
Vous êtes difficile en certitude, si vous doutez que l’expansibilité de l’air soit une propriété de l’agrégat. Vous voyez que je traduis votre phrase et que je ne regarde point l’élasticité comme synonyme d’expansibilité, ni le mot de masse, comme synonyme de celui d’agrégat. Au reste, cela me paraît démontré autant que les choses physiques le sont.
Vous allez donc choisir un chimiste. Dans ce genre, l’Académie a quelquefois, en choisissant, pris le pire. Depuis la sottise qu’elle a faite de rejeter Rouelle et d’Arcet pour prendre Sage[25], elle n’avait rien de mieux à faire que de les élire malgré le parti qu’ils avaient pris de ne plus se présenter ; cette réparation leur était due et l’Académie aurait eu des hommes qui lui auraient fait honneur. Baumé, au reste, est homme de mérite.
Adieu, M., recevez les assurances de mon amitié.
XIX. (Détails divers. — Le marquis de Paulmy.)
Limoges, 29 décembre.
Ma goutte, M., ne vaut pas la peine de murmurer contre la Providence et il y a dans ce monde beaucoup de choses auxquelles j’ai bien plus de peine à me résigner. J’espère qu’elle m’a quitté tout à fait. Je lui demande du moins quartier jusqu’à Paris où je trouve ses inconvénients beaucoup moins sensibles.
Mlle de Lespinasse m’a mandé l’aventure de Voltaire ; il me semble que l’évanouissement gâte un peu le miracle. J’ai peur que les tragédies ne ressemblent un peu aux bonnes fortunes. Ces Pélopides ont bien de l’analogie, mais il faut avouer que les pièces fugitives ont encore toute la vigueur de la jeunesse. Ces trois siècles dont vous me parlez pourront nous valoir quelque morceau d’indignation.
Je ne suis point étonné que vous ayez contre vous à l’Académie le Paulmy[26]. Mais ces gens-là ont tant de moyens de nuire et tant d’activité à les employer que je suis fâché qu’il se soit avisé d’être votre ennemi.
Adieu, M., vous pourrez encore m’écrire dimanche ; mais ce sera la dernière fois. Mille choses à nos amis. Je vois avec peine que vos inquiétudes sur Mlle de Lespinasse reviennent.
XX. (Détails divers.)
Limoges.
Hélas, M., mon départ était fixé à aujourd’hui et me voilà encore réduit à ne partir que la semaine prochaine, tandis que les chemins semblaient s’être aplanis pour mon voyage. Le retard ne sera pourtant pas long ; car tout mon monde est parti et même la plus grande partie de mes papiers. J’ai d’ailleurs grande envie de ne pas attendre le dégel.
J’ai lu avec un vrai plaisir l’Éloge de Racine. Voici ma lettre de remerciement à l’auteur dont je ne sais pas l’adresse. Je suis enchanté que vous ayez fait connaissance avec Mlle d’Enville : ce sera une occasion de plus pour vous voir souvent.
Je vous remercie de vos nombres : mais quoique vous vous soyez on ne peut mieux adressé, il y a pourtant erreur dans le logarithme de 241 multiplié par 84. Mais cela ne fait rien parce qu’il n’y en a point dans le chiffre correspondant. Mais ce qui me fâche, c’est que je n’ai précisément que ce que j’avais par Rivard. Je croyais que les tables de Wlac contenaient beaucoup plus de décimales et me donneraient au moins un chiffre de plus pour chacun des nombres correspondants aux 84es puissances de 240 et de 241, ce qui m’aurait suffi pour mon objet.
Je ne sais trop si les éloges du roi de Prusse doivent consoler les philosophes des injures des cuistres et des fripons. Ne pourrait-on pas dire, au contraire, que ces injures peuvent consoler des éloges ?
Je vous remercie des bonnes nouvelles que vous me donnez de Mlle de Lespinasse. Vous savez combien vous devez compter sur mon amitié.
—————
[1] Cette lettre a dû être écrite à Clermont ; nous avons modifié légèrement la fin du 2e paragraphe pour le rendre compréhensible.
[2] Condorcet avait écrit à Turgot qu’il reprendrait ce sujet avec lui.
[3] On lit dans les Lettres de Mlle de Lespinasse à Condorcet :
14 juin. — M. Turgot m’a écrit, il vous croyait encore à Paris.
Vendredi (juillet). — Vous manquez bien à M. Turgot qui est bien mal instruit de ce qui se passe depuis votre départ.
26 juillet. — M. Turgot vous envoie des graines de raves qu’il a adressées à M. Bertin ; on a écrit à M. Parent, premier commis de M. Bertin ; on ne reçoit ni réponses, ni raves.
23 août. — M. Turgot est dans une grande privation depuis votre départ.
[4] Condorcet avait écrit le 14 juin : « Vous êtes bien heureux d’avoir la passion du bien public et de pouvoir y satisfaire ; c’est une grande consolation et d’un ordre supérieur à celle de l’étude ».
[5] Turgot, en vue de répandre dans le Limousin l’art de la sparterie, avait demandé à Condorcet de lui envoyer un vannier picard.
[6] Essai sur les probabilités en fait de justice, par Voltaire.
[7] Le maréchal de Richelieu pour qui Voltaire avait écrit Les Cabales.
[8] De Bréquigny (1716-1793) de l’Académie des Inscriptions (1759) qui venait d’être élu à l’Académie française.
[9] Mme du Châtelet (1706-1749), mathématicienne, amie de Voltaire.
[10] Saint-Lambert.
[11] Voltaire.
[12] Par Voltaire.
[13] De l’Académie des Sciences que sollicitait Condorcet.
[14] Cette formule que, paraît-il, Turgot avait demandée, est n’(n+1)(n+2) / 6 = (n3+2n2+2n) / 6 que l’on trouve « en observant, disait Condorcet, que ces nombres doivent être exprimés par une fonction de n, telle qu’en y mettant n+1 au lieu de n, la différence soit (n2+2n+1)/2, formule pour le nombre triangulaire, qui est le (n+1)ème. »
[15] Mathématicien écossais (1671-1721).
[16] Mathématicien hollandais (1688-1742).
[17] Dans son ouvrage sur la cristallisation, De Romé de Lisle (1736-1790) avait protesté en tête qu’il ne prétendait pas que la géométrie put jamais expliquer ce phénomène. « Je ne sais, disait Condorcet, s’il a le droit de faire les honneurs de la géométrie, mais il a mis cette phrase pour contenter l’école de Rouelle ».
[18] Jean Dollond, opticien anglais.
[19] Voir tome I, p. 538.
[20] Lettre de Condorcet du 22 novembre : « Voilà une expérience que M. Sage fera ces jours-ci avec moi. Je mettrai de la chaux de plomb avec du charbon dans une cornue dont le bout luté sera garni d’un tube plongé dans l’eau de chaux. Si en réduisant la chaux de plomb, la chaux se précipite, ce sera un indice que la rephlogistication du plomb produit ce que nous appelons air fixe, etc. »
[21] Réponse d’Horace à Voltaire, par La Harpe.
[22] D’Alembert et Condorcet avaient été désignés par l’Académie des Sciences pour examiner un ouvrage de Montagne. Condorcet pensait que si cet ouvrage devait être imprimé, il fallait y ajouter une démonstration de sa méthode d’approximation.
[23] Les Lois de Minos, tragédie de Voltaire, non représentée.
[24] Cottereau Duclos, médecin de Louis XIV, mort en 1715.
[25] Sage (1740-1824), qui fut adversaire de Lavoisier.
[26] Marquis de Paulmy d’Argenson, académicien honoraire.

Laisser un commentaire